相関関係分析の事例

2019.02.01 Selfish Study 0 Comment boff 0 view

具体的なデータを使って相関関係の分析をしてみたいと思います。
Excelを使いますが、CORREL関数やPEAESON関数を使わず、途中の計算過程を踏まえながら相関係数を算出したいと思います。
使用したデータは、2018年度の「地域最低賃金」（厚生労働省）と2014年経済センサスの「都道府県別雇用者数」（総務省）です。

地域最賃一覧

下表は、2018年度の地域最賃を高い順位に並べ替えた一覧表です。

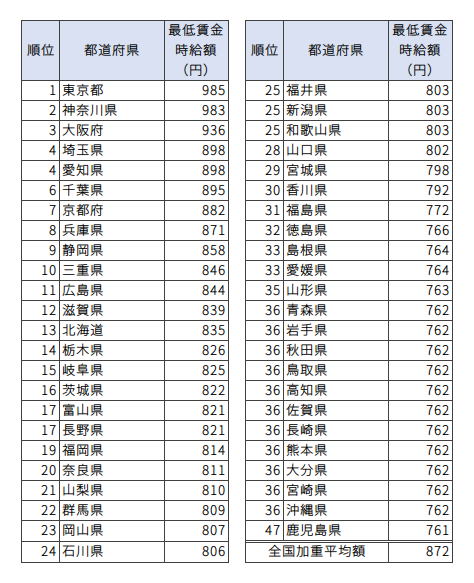
「全国加重平均額」とは、都道府県ごとの雇用者数を加味した平均値で、実際に最低賃金が適応になる人数の平均額ということになります^†1。
雇用者数の値については、2014年経済センサスの「都道府県別雇用者数」を使用しています。

都道府県別の最低賃金と雇用者数の関係

次に、地域別最賃と都道府県ごとの雇用者数の関係を散布図に表してみました。

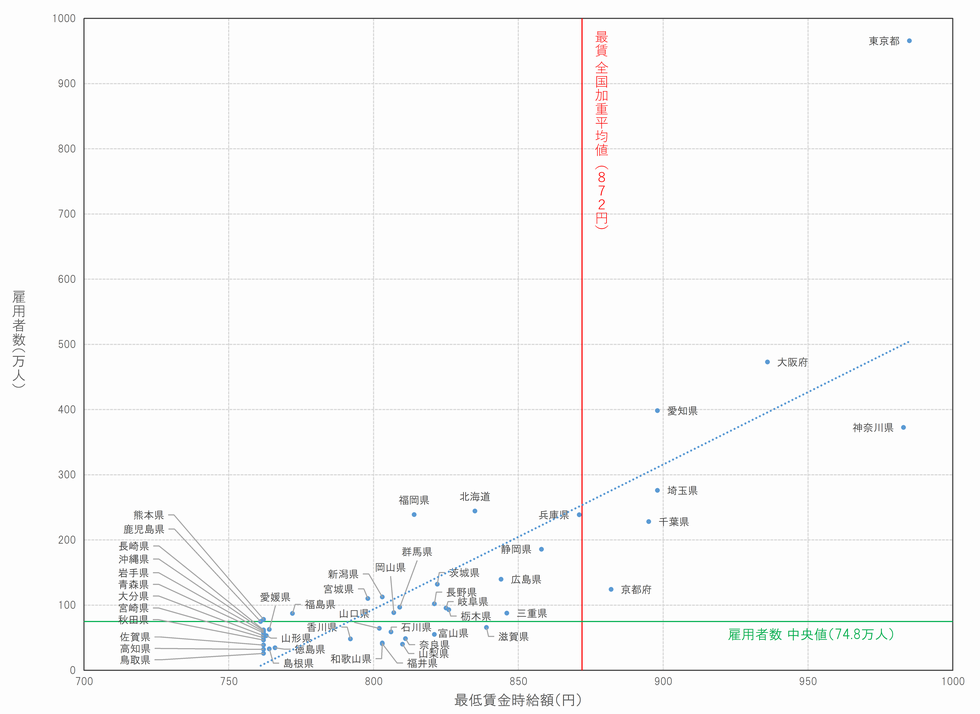
縦軸が雇用者数、横軸が最低賃金時給額です。
赤い縦線は最賃の「全国加重平均値（872円）」、緑の横線は「雇用者数中央値（74.8万人）」の水準をそれぞれ示しています。
散布図を見ると、東京都が最賃も雇用者数も飛び抜けて高いです。
最賃と雇用者数のどちらの水準も超えているのは、7都府県（東京都、神奈川県、大阪府、愛知県、埼玉県、千葉県、京都府）だけだということがわかります。
また、大阪府は神奈川県と比べて、雇用者数は多い割に最賃が低くなっています。

一方、北海道と福岡県は、雇用者数は京都府よりも高く、埼玉県や千葉県と同程度であるにもかかわらず、最賃に関してはかなり低いですね。

さて散布図を見ると、最低賃金が高いと雇用者数も高いといった正の相関関係がありそうなのですが、実際に相関係数を出して検証してみましょう。

相関係数の算出方法と手順

相関係数の算出式は次のとおりです。

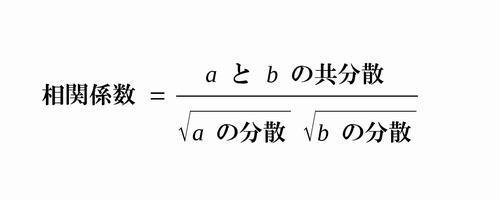
式のaとbはそれぞれのデータのことで、例えば今の場合、「a」が「地域最低賃金」、「b」が「都道府県別雇用者数」です。
相関係数を算出するのには、「aとbの共分散」「√aの分散」「√bの分散」^†2が必要です。
「aとbの共分散」は、「aの偏差×bの偏差」の平均で求めることができます。
「√aの分散」は「aの偏差²」の平均、「√bの分散」は「bの偏差²」の平均でそれぞれ求めることができます。
「偏差」は、データの平均値から個々の値を引いた値です。

aとbのデータについて、「偏差」「分散」「共分散」の算出結果は次の表のようになります。

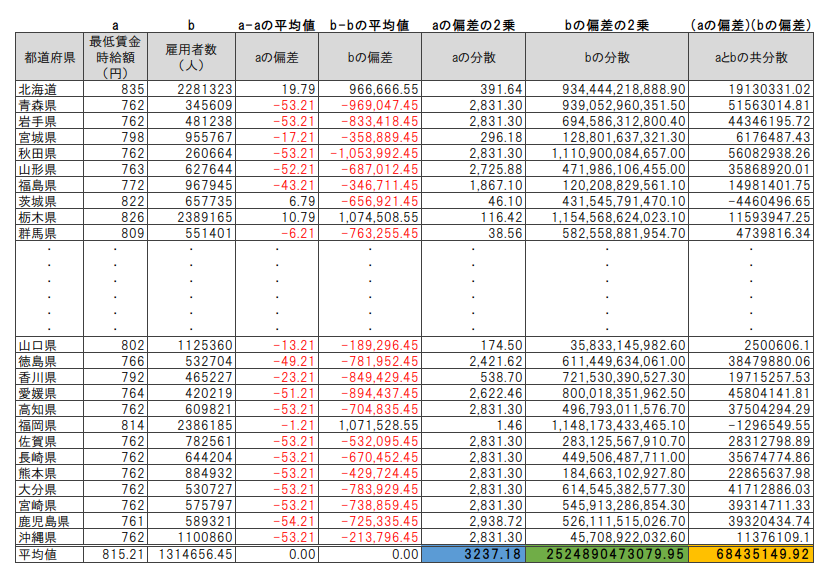
上の表から、aの分散＝3,237.18、bの分散＝2,524,890,473,079.95、aとbの共分散＝68,435,149.92が得られました。
これらの値を先ほどの相関係数の定義式に代入し計算すると、相関係数は「0.76」と求めることができました。

相関係数とは、2種類のデータ間の相関の強さの度合いを示す値で、必ず-1から+1の間の値をとります。
相関係数は、+1に近いほど正の相関が強い、-1に近いほど負の相関が強い、0に近いほど相関はないとされます。
「正の相関」とは「aが大きければbも大きい傾向がある」、「負の相関」とは「aが大きければbは小さい傾向がある」ということです。
相関係数の度合いに関して、一般的な目安は次のとおりです。

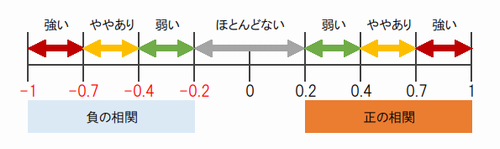
したがって、「0.76」は「強い正の相関がある」ということ意味します。

相関係数の注意すべきポイント

多くの統計データにも言えることですが、相関係数は異常値（外れ値）に影響されやすいとされています。
飛び抜けた値に引っ張られ、正確な測定ができないケースがあるということです。

例えば今回使用したデータでいうと「東京都」は異常値と言えます。
異常値を含んだデータから相関係数を算出するには、順位データから相関係数を求めるノンパラメトリック法（スピアマンの順位相関係数）を用いた方がより正確な値が得られるとされています。
試しに今回のデータを、BDAstyleさんの「スピアマンの順位相関係数の計算」をお借りして計算してみると、相関係数は「0.57」でした。

さらに、相関関係は因果関係と混同されやすいという問題があります。
例えば、今回の分析結果から正の相関が認められました。
では「最低賃金が高くなれば、雇用者数も増加する」と言えるでしょうか？
賃金が高いところに求職者が集まるという因果関係は否定できませんが、雇用者数が増加する要因（地域の人口規模、事業所数、企業規模、産業構造、企業ブランドイメージなど）は他にもあります。
逆に、「雇用者数が増えれば、最低賃金も高くなる」と言えるでしょうか？
実際、最低賃金の引き上げは、その地域の物価などが大きく影響しているので、この仮説はかなり無理があります。
つまり、相関係数は統計学や数学としての値であって、一方が原因でもう一方が結果であるという因果関係とは区別して捉える必要があります。