「検定」について考える

2019.02.13 Selfish Study 0 Comment boff 0 view

検定について、その考え方（理屈）をまとめてみました。

検定とは？

検定とは、得られたデータに偏りや差があるかどうかを、検定手法で算出した値の大きさによって検証する統計学的方法のことです。

検定の使い分け

代表的な検定手法としては、「カイ二乗検定」「t検定」「分散分析」があります。
どの種類のデータのときにどの検定を用いるのかをフローチャートで簡単に整理してみました。

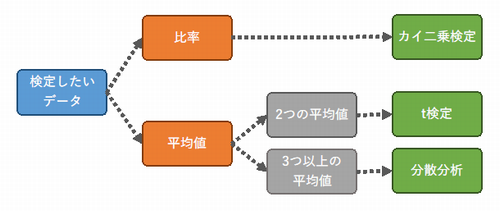
検定したいデータが比率の場合は、カイ二乗検定。
平均値の場合は、2つのデータならt検定、3つ以上なら分散分析を用います。

検定の手順

検定は次のような手順で行われます。

仮説の設定・・・帰無仮説と対立仮説の設定
有意水準の設定・・・5％か1％か任意で決定
検定値の計算・・・それぞれの検定手法から検定値あるいは有意確率を算出
仮説の検証・・・有意水準と検定値あるいは有意確率を比べて帰無仮説を棄却するかどうかを判断
検定の結果・・・帰無仮説を棄却し対立仮説を採用／帰無仮説は棄却できず何も言えない

帰無仮説と対立仮説について

統計学で検定をする場合、相反する2つの仮説を立て、一方の仮説を否定することで、もう一方の仮説を採用するといった回りくどい方法をとります。
前者を「帰無仮説」、後者を「対立仮説」と呼び、「帰無仮説を否定する」ことを帰無仮説を「棄却する」と言います。

帰無仮説が棄却され対立仮説が採用された場合は「有意差がある」と言い、帰無仮説が棄却されなかった場合は「有意差がない」と表現します。

例えば、性別による数値の差について検定する場合、次のように仮説を立てます。

帰無仮説・・・性別による数値に差はない
対立仮説・・・性別による数値に差がある

「性別による数値に差はない」という仮説（帰無仮説）を前提として、調査データの得られた確率を計算します。
結果その確率が低ければ、帰無仮説は起こるはずのないきわめて稀な事態として棄却され、対立仮説の「性別による数値に差がある」が採用されます。

もちろん調査データの得られた確率が高い場合もあります。
その場合は、得られたデータには確率的に必然性があるので帰無仮説は棄却できず、「性別による数値に差はない」という帰無仮説はそのまま残ることになります。

調査データの得られた確率を「有意確率」と言い、それが高いか低いかは「有意水準」を基準に判断されます。
有意水準は検定する人が任意に設定でき、統計学では「5％」にするのが一般的で、より厳密に検定したい場合は「1％」に設定します。

有意水準=棄却域＝危険率

有意水準は、有意確率との関係から帰無仮説を棄却するかどうか判定するので、「棄却域」と呼ばれます。
有意確率が小さい場合は「棄却域内に有意確率がある」、大きい場合は「棄却域内に有意確率はない」「有意確率は棄却域外である」といった言い方をします。

また、有意水準は、有意確率がきわめて稀に起こり得た確率かどうかを判断する基準ですが、裏を返せば5％あるいは1％の低い確率でも偶然か必然かの判断ミスの余地を残していることを意味しています。
例えば、有意確率が3％のとき、もし有意水準5％なら棄却され有意差ありと判断されますが、1％なら棄却されませんので有意差ありという判断は間違っていたことになります^†1。
その逆も然りで、もし1％の場合、5％なら有意差ありと判断できるのに、いつまでも帰無仮説を棄却できずに判断を間違っていることになります^†2。
したがって、5％あるいは1％の確率で判断を間違う可能性があるという意味で、有意水準は「危険率」とも呼ばれます。

検定結果を解釈する際の注意

検定における危険率は、「検定の結果は絶対ではない」ことも意味しています。
あくまでも仮説の「確からしさ」の根拠を得るだけですから、帰無仮説が棄却できなかったから「絶対にデータに偏りや差はない」と言い切れるものでもありませんし、帰無仮説が棄却されたからといって「対立仮説が絶対に正しい」とも言い切れません。
ですから、検定の結果はよほどのことがない限り断定的な解釈は避け、「有意差が認められる」とか「有意差は認められない」といった表現に留めるのが一般的です。
とりわけ有意差がない場合は、帰無仮説が棄却するだけの根拠が不十分なだけで、まだ何も言えない中途半端な状況に過ぎないということに留意すべきです。

さらに、検定結果は、得られたデータに「何らかの偏りが差があることだけ」を検証したに過ぎず、その偏りや差の具体的な中身を明らかにしたことになりません。
有意差の中身について分析をするには、残差分析や相関分析などを用いることになります。

有意差の有無とその意義

さて検定の結果について、有意差がない場合には意味がないのでしょうか？
答えは、完全にNoです。

「有意差があるだろう」という仮説のもとで検定するので、結果、有意差なしのとき、想定を裏切られて残念に思う気持ちはわかります。
しかしながら、有意差の有無にかかわらず、検定から得られたどちらの結果も意義としては同等です。
有意差があった場合は言うまでもありませんが、有意差がなかった場合も「有意差がないということを発見した」ことの意義は大きいです。
言い換えれば、第一種の過誤（例えば、誤認逮捕）を回避することに成功したと言えるからです。

思っていた結果が得られなかったからといって、有意確率を見て有意水準を引き上げるのは本末転倒です。
ましてや都合の悪いデータをオミットしてデータを改ざんすることはご法度ですし、科学的な分析手法としての信頼を根本から失うことになります。

統計調査全般に言えることですが、結果は謙虚に受け止める姿勢が大事ですね。