Marble-Lab

今年一年、日本では「年金」が大きな社会問題となった。
基礎年金番号と統合されていない、いわゆる宙に浮いた年金記録が5,000万件あり、この解決に関して記録の照合が焦眉の課題となっている。
この年金問題についてその是非を問うことはやぶさかではないのだが、ここでは統計学的（？）に少し整理してみたいと思う。

まず記録不明になっている5,000万件とはいったいどういった値なのだろうか。
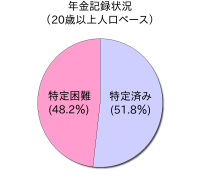
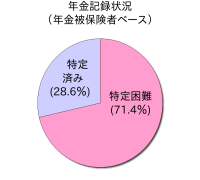
平成17年の20歳以上の人口が約1億366万6,000人だとすると、5,000万件は48.2％とほぼ2人に1人の割合にあたり、年金被保険者約7,000万人をベースにすると71.4％が記録不明ということなる。
問題発覚当初、この5,000万件の名寄せ作業を年内に完了させるという話だった。
もし年間の労働日数が240日^†1だとすると、1日あたり20万8,333件の照合作業をしなければならない。

また最近になって5,000万件のうち7,840件のサンプル調査を実施し、年金記録の特定困難な割合が38.5％であることが明らかとなった。
サンプル（標本）調査とは、母集団の一部を抽出して調査し、その調査結果から母集団の状態を推定する統計学的調査手法のことである。
この調査結果から推定すると、5,000万件のうち38.5％、つまり1,925万件が特定困難だということがいえる（点推定）のだが、実際のところサンプル調査には必ず標本誤差がつきまとう。
サンプル調査は先ほども説明したように、母集団の一部を抽出した調査であるから、たまたま抽出したサンプルの結果が38.5％だったということであって、また新たにサンプル抽出をして調査をしたら同じ結果になるかもしれないしそうではないかもしれない。
言い換えると、サンプル調査はその偶然性（誤差）から逃れられないのである。

7,840件のサンプル調査に話を戻そう。
サンプル調査には誤差があるという前提で、ではいったいどの程度の誤差があるのだろうか。
標準偏差（データのバラつき）を求めると43.1^†2。
よって、95％の信頼度で区間推定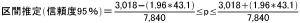^†3すると、37.4％から39.6％の間に母集団の比率があると推定される。
これは38.5±1.1％の誤差があるということであって、年金記録の特定が困難な件数は実際のところ±55万件の幅があるということがわかる。
「1％程度の誤差」といわれるとたいした問題には感じられないが、「前後55万件の幅」ということになれば、やはり5,000万件という数字はきわめて深刻な数字に感じられるのである。